벌써 6월이 다 지나갔네요!
그동안 좀 무리했더니 몸이 힘들어서 이번 주말은 집에서 푹 쉬었답니다...^^
다음 주에는 미니 팀 프로젝트가 있기 때문에 미리 쉬어야겠더라구요.
해야 할 일은 많은데... 체력도 함께 관리해야 해서 이래저래 신경써야 하는 일들이 정말 많네요.
그래도 하나씩 할 일들 쳐내다 보면 어느 순간 지금보다 발전해 있겠죠?
미래에 성장해 있을 저를 생각하면서 힘내야겠습니다!

● 성취
이번 주에는 딥러닝 파트를 배웠습니다.
딥러닝 업계가 발전한 역사를 베이스로 퍼셉트론, DNN, CNN 등을 다뤘습니다.
또한 딥러닝 모델을 학습시킬 때 사용하는 기법들도 습득했습니다.
경사하강법, 다양한 옵티마이저들, 드롭아웃 등을 익혔습니다.
이제 본격적으로 AI 개념을 다뤄서 몹시 설레네요...^^
● 개선 & 학습
이번 주도 개선이 곧 학습이고, 학습이 곧 개선이라고 느껴져서 하나로 합쳤습니다...^^
당분간은 두 테마들을 하나로 합쳐서 글을 작성할 것 같네요.
# 퍼셉트론(Perceptron) & MLP(Multi-Layer Perceptron) & ANN(Artificial Neural Network)
'퍼셉트론'은 로젠 블렛이 1957년 고안한 알고리즘으로, 인간의 뇌 신경세포가 동작하는 과정에서 영감을 받아 만들어졌습니다.
로젠 블렛이 제안한 퍼셉트론을 사용하면 입력 데이터를 2개 카테고리 중 하나로 분류할 수 있습니다.
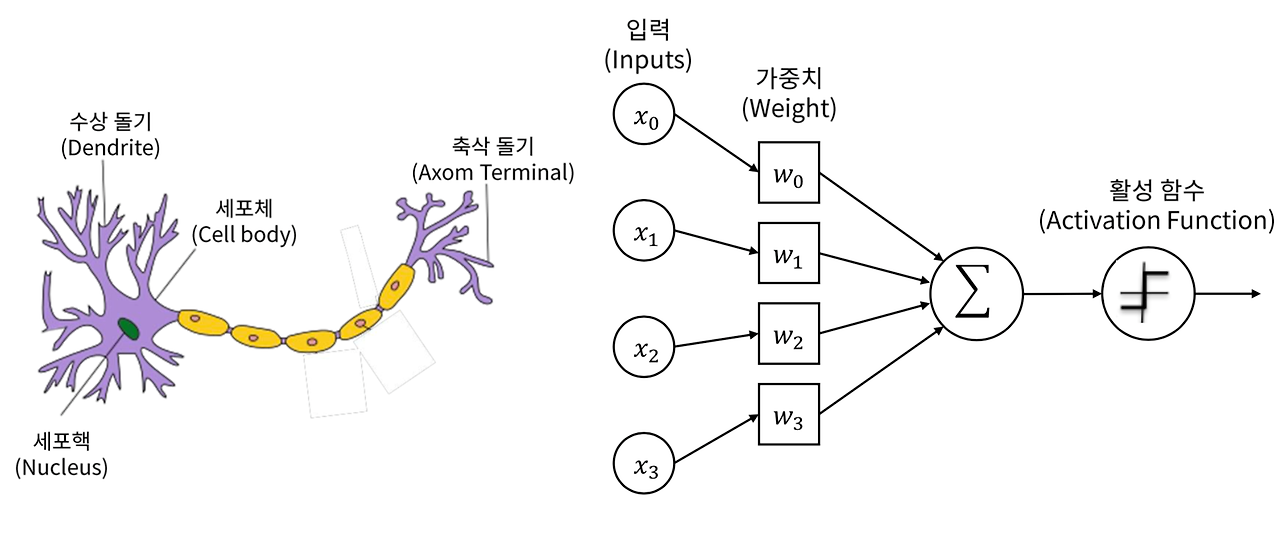
왼쪽은 인간의 뇌 신경세포이고, 오른쪽은 퍼셉트론을 나타낸 사진이에요!
퍼셉트론은 입력층 1개, 출력층 1개, 입력층과 출력층 사이에 존재하는 가중치들로 구성되어 있습니다.
입력층에서는 몇 개의 입력을 받을 것인지 설정이 가능한데요.
이 입력값 개수 설정에 따라 가중치 개수도 정해집니다.
입력층에서 5개의 입력 값을 넣기로 결심하면, 가중치 개수 역시 5개로 설정해야 합니다.
그리고 각각의 입력값은 대응하는 가중치와 곱한 뒤, 곱한 각각의 값을 모두 더합니다.
이렇게 더한 값은 활성함수에 대입함으로써 활성 여부를 결정해요.
활성 기준 미달은 0으로, 활성 기준을 넘겼을 때는 1로 판정합니다.
퍼셉트론 아이디어 정말 신기하죠?
그런데 문제는... 이 퍼셉트론이 아래와 같은 문제를 풀지 못한다는 단점이 존재해요.
아래 위치에 존재하는 세모와 동그라미를 분류하는 문제인데, 이걸 'XOR 문제'라고 부른답니다!

이 문제는 퍼셉트론을 한 층 더 쌓음으로써 해결했어요.
XOR 문제를 해결한 새로운 퍼셉트론을 MLP(Multi Layer Perceptron)라고 부릅니다.
위에서 설명한 퍼셉트론과 MLP는 ANN(Artificial Neural Network) 개념을 구성하는 기반입니다.
다시 말해서 인공지능을 지탱하는 첫 뼈대라고 할 수 있지요.
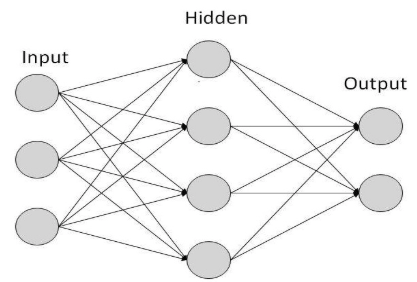
ANN은 위 그림처럼 Input 레이어 1개, Hidden 레이어 1개, Output 레이어 1개로 구성되어 있습니다.
# DNN(Deep Neural Network)
위에서 언급한 ANN은 단점이 있습니다.
학습 시 최적의 가중치 값을 찾기 어려우며, 학습 시간이 느리고, 과적합(Overfitting) 문제가 존재하거든요.
과적합은 주어진 데이터셋에만 집중하느라 일반화 능력이 떨어지는 것을 의미합니다.
적당히 융통성 있는 사람이 일을 잘하는 것처럼 인공지능도 마찬가지입니다.
과적합 문제가 발생한 모델은 융통성이 부족한 모델이라고 볼 수 있어요.
이를 해결하기 위해 기존의 ANN에 은닉층을 하나 이상 더 추가했답니다!
은닉층을 더 추가하게 됨으로써 인공지능은 다양한 구조를 더 잘 파악하게 되었어요.
직선으로 분류할 수 있는 케이스 뿐만 아니라, 곡선으로 분류할 수 있는 능력도 갖추게 된 거죠!
참고로 DNN은 아래 그림처럼 생겼어요.
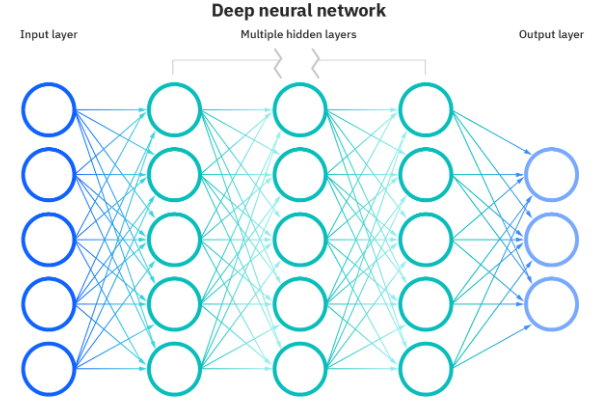
# CNN(Convolutional Neural Network)
DNN이 도입됨으로써 현실 속 많은 문제들을 풀 수 있게 되었지만, 이미지 인식 등의 영역에서는 여전히 한계가 존재했어요.
이 문제를 해결하기 위해 커널(kernel)을 도입했어요.
커널은 다른 말로 필터(filter)라고 부르기도 합니다.
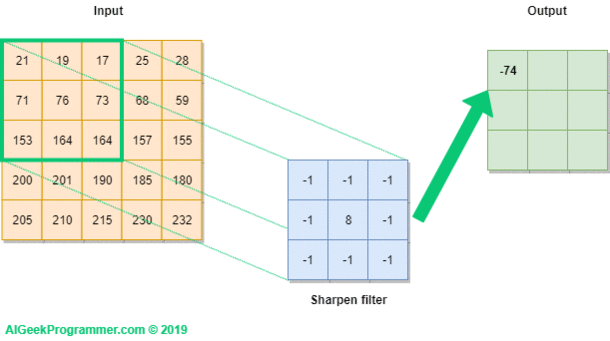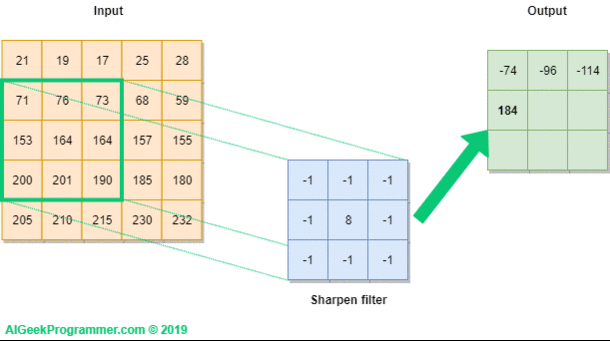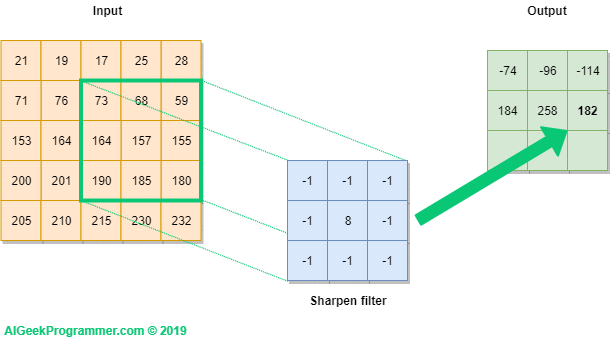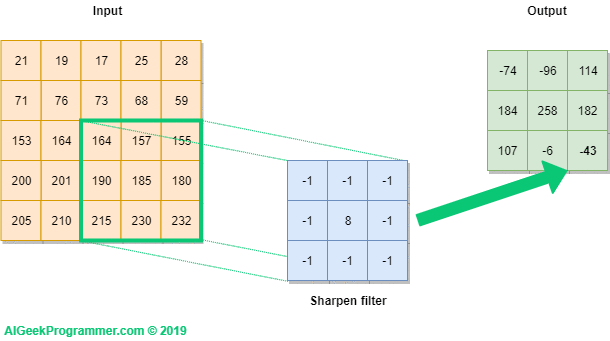
커널을 사용한 연산 방식은 위 그림과 같습니다.
이렇게 연산하면 커널의 특성을 반영해서 이미지 픽셀들을 다룰 수 있어요!
근데 문제는 이렇게 커널을 이용해서 계산을 하면 Input 사이즈에 비해 Output의 크기가 작아지죠?
이렇게 커널을 여럿 사용하다 보면 정말 끝도 없이 작아지겠어요~
연구자들은 사이즈 축소 문제를 어느 정도 방지하기 위해 패딩(padding) 방식을 도입했어요.
인간이 입는 패딩 점퍼처럼 이차원 행렬 데이터 외곽에 0을 덧씌워 주는 것을 의미합니다.
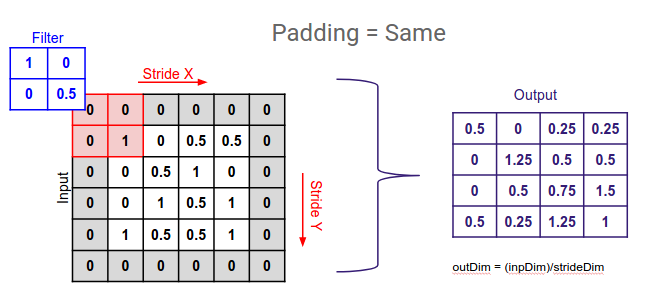
위 그림처럼 2차원 행렬 주변에 0을 덧씌웠더니, 필터를 사용해서 연산을 해도 Output 사이즈가 줄어들지 않는군요!
필터와 패딩 말고도 CNN에서는 중요하게 다루는 개념이 또 있습니다.
바로 풀링(pooling)인데요.
풀링을 사용함으로써 필터를 사용해서 계산한 2차원 행렬 값을 요약할 수 있게 됩니다.
풀링에는 크게 두 종류가 있습니다.
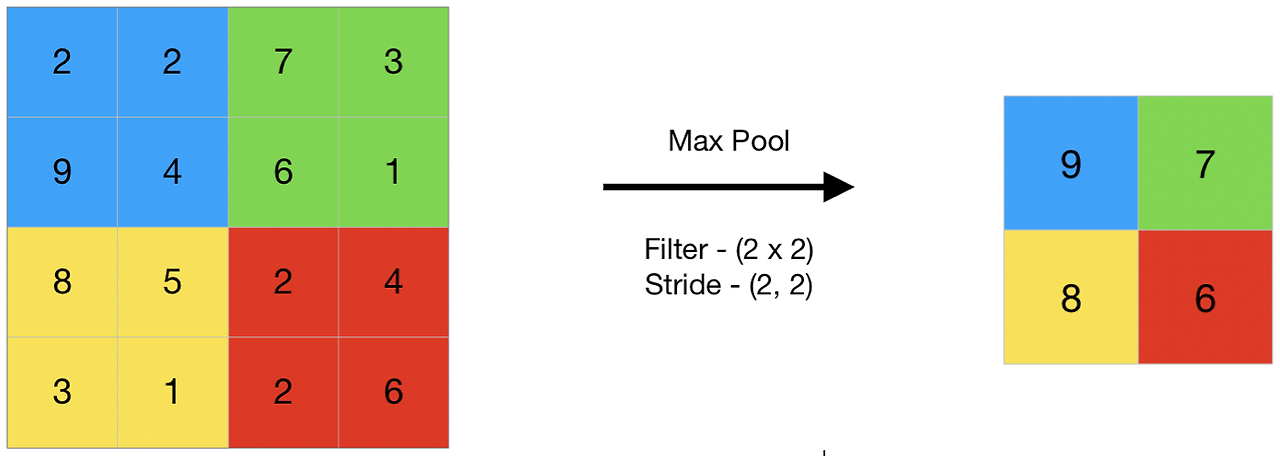
가장 먼저 Max Pool이 있습니다.
Max Pool을 사용하면 단위 영역 내의 최댓값을 기준으로 요약할 수 있어요.

다음으로는 Average Pool이 있습니다.
Average Pool을 사용하면 단위 영역 내의 평균값을 기준으로 요약이 가능합니다.
이렇게 커널(=필터), 패딩, 풀링을 섞어 가면서 CNN 연산을 하게 되면, DNN보다 좋은 성능으로 이미지 인식을 할 수 있어요!
# 손실함수
딥러닝 모델의 성능을 개선하기 위해서는 어떠한 기준점이 필요합니다.
이 기준점 역할을 하는 것이 바로 '손실함수'인데요.
손실함수는 예측 값과 실제 값 사이에 존재하는 차이를 측정합니다.
AI 모델은 손실함수 값을 최소화시킬 수 있는 지점 찾기를 목표로 학습합니다.
그래야 예측과 실제 사이의 값 차이가 많이 안 나겠죠?
즉, 손실함수는 AI 모델 학습에 있어서 나침반이라고 볼 수 있습니다.
# 옵티마이저(Optimizer)
앞에서 AI 모델은 손실함수 값을 최소화시킬 수 있는 지점을 찾는 것을 목표로 한다고 했지요?
손실함수가 나침반이라면, 옵티마이저는 항해 방식이라고 생각할 수 있습니다.
나침반이 같은 방향을 가리키더라도, 항해 방식에 따라 목적지 도달 시간이 달라집니다.
그리고 특정 항해 방식이 정답이라고 할 수 없는 것처럼 옵티마이저 사용에도 정답이 없습니다.
(보편적으로 Adam이 좋다고 알려져 있지만 그게 늘 정답은 아닙니다.)
최근에 나온 항해법이 우수할 가능성이 높지만, 그게 꼭 모든 상황에 맞는 것은 아닌 것처럼요.
문제 상황을 살펴본 다음에 각자 케이스에 맞게 옵티마이저를 선정해야 합니다.
저는 이게 마치 인생처럼 느껴집니다.
- 경사하강법 (GD, Gradient Descent)
- '경사하강법'은 현재 손실함수 지점에서 기울기를 측정하여, 기울기의 반대 방향으로 일정 학습률 만큼 업데이트하는 방식입니다.
가장 베이직한 방법이라고 볼 수 있지만, 빅데이터를 기반으로 AI를 학습시킬 때 비효율적이라 딥러닝 api에 거의 없더라구요....!
- '경사하강법'은 현재 손실함수 지점에서 기울기를 측정하여, 기울기의 반대 방향으로 일정 학습률 만큼 업데이트하는 방식입니다.
- 확률적 경사하강법 (SGD, Stochastic Gradient Descent)
- 앞에서 언급한 경사하강법은 전체 데이터를 모두 고려한다는 단점이 있습니다.
따라서 데이터 크기가 너무 커지면 계산량 역시 헤비해질 수밖에 없어요.
이런 점을 의식하여 '확률적 경사하강법'이 탄생했습니다.
왜냐하면 확률적 경사하강법은 일부 데이터(=미니 배치)만 사용해서 연산하거든요.
아래에서 다룰 옵티마이저들은 모두 SGD를 기반으로 작동합니다.
따라서 딥러닝 api에서 가장 베이직한 옵티마이저를 'SGD'라고 생각하면 될 것 같습니다!
- 앞에서 언급한 경사하강법은 전체 데이터를 모두 고려한다는 단점이 있습니다.
- 모멘텀 (Momentun)
- '모멘텀'은 앞에서 언급한 확률적 경사하강법에서 이전 업데이트 방향까지 고려해서 관성을 부여한 방법입니다.
+) 참고로 관성을 영어로 Momentum이라고 부릅니다.
확률적 경사하강법에 비해 조금은 보수적으로 접근하는 방식이라고 생각할 수 있어요.
따라서 업데이트의 안정성까지 모두 챙길 수 있게 되었습니다.
급진/보수는 특성의 차이일 뿐, 완벽한 정답은 없으니 상황에 맞게 옵티마이저를 고르면 됩니다!
- '모멘텀'은 앞에서 언급한 확률적 경사하강법에서 이전 업데이트 방향까지 고려해서 관성을 부여한 방법입니다.
- 네스테로프 모멘텀 (Nesterov momentum)
- 앞에서 소개한 모멘텀은 과거와 현재를 함께 고려한 옵티마이저였습니다.
반면에 '네스테로프 모멘텀'은 현재와 미래를 동시에 고려합니다.
어느 순간에 배팅하는 것이 좋을지 결정하는 것은 사용자의 몫입니다...^^
- 앞에서 소개한 모멘텀은 과거와 현재를 함께 고려한 옵티마이저였습니다.
- 아다그라드 (Adagrad)
- '아다그라드'는 파라미터별로 학습률을 조정하는 방식입니다.
업데이트가 많이 이루어진 파라미터의 학습률은 낮추고, 적게 이루어진 파라미터의 학습률은 높이거든요.
마치... 사람들이 살고 있는 세상에서 소득 기준으로 시행되는 정책들이 생각나네요.
- '아다그라드'는 파라미터별로 학습률을 조정하는 방식입니다.
- 알엠에스프롭 (RMSProp)
- 아다그라드는 시간 정보를 고려하지 않고 파라미터별로 학습률을 조정한 방식입니다.
다시 말해서 먼 과거와 가까운 과거를 동일한 취급을 한다고 볼 수 있습니다.
'알엠에스프롭'은 이를 방지하기 위해 지수이동평균을 도입했습니다.
이를 통해 먼 과거는 조금 반영하고, 가까운 과거를 많이 고려할 수 있게 되었습니다.
- 아다그라드는 시간 정보를 고려하지 않고 파라미터별로 학습률을 조정한 방식입니다.
- 아담 (Adam)
- '아담'은 모멘텀과 알엠에스프롭을 결합한 방식입니다.
따라서 모멘텀처럼 과거와 현재 목적함수 기울기 방향을 고려할 뿐만 아니라, 알엠에스프롭처럼 시간 정보를 신경 쓰면서 파라미터별로 학습률을 조절할 수 있게 되었습니다.
위에서 설명한 옵티마이저들 중에서 가장 최근에 나왔기 때문에, 보편적으로 가장 성능이 좋다고 하네요.
- '아담'은 모멘텀과 알엠에스프롭을 결합한 방식입니다.
일단 보편적으로 성능이 좋은 아담을 문제에 적용한 뒤, 상황에 맞게 다른 옵티마이저를 적용해 보는 것을 추천합니다!
아무래도 보편성이 늘 정답을 의미하는 것은 아니잖아요~
여러분의 상황에 맞는 항해법을 선택하시면 됩니다 ^_^
# 드롭아웃(Drop-out)
DNN에서 과적합 개념을 설명했던 거 기억하시나요?
ANN에 비해 DNN이 과적합 현상을 개선한 건 맞지만, 완전히 개선한 것은 아니랍니다.
과적합 문제를 해결하기 위해 몇몇 뉴런들의 작동을 멈추게 하는 경우도 있답니다.
이것을 '드롭아웃'이라고 해요.
근데 무작정 몇몇 뉴런들의 작동을 멈추게만 하면 성능이 떨어지겠죠?
이를 방지하기 위해 앙상블 기법을 섞어서 사용합니다.
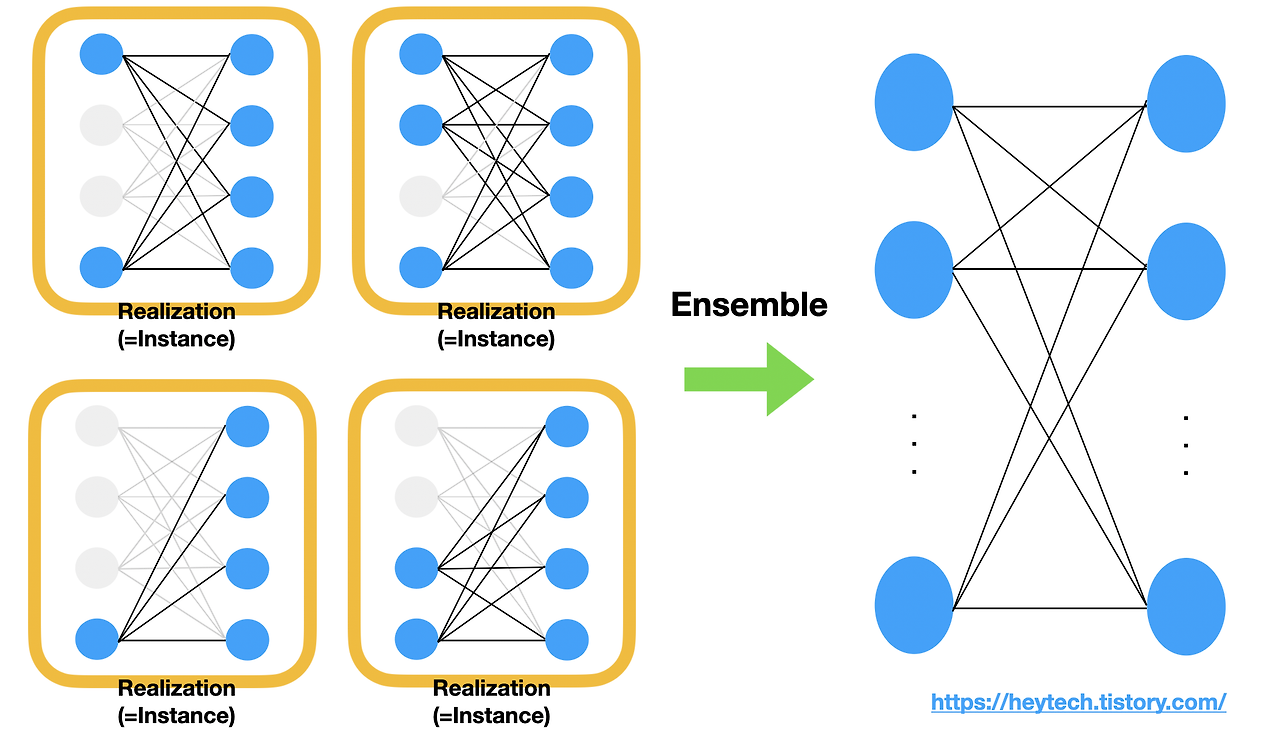
다시 말해서 몇몇 뉴런들이 멈춰 있는 케이스들을 여러 개 조합하여 적절한 선을 찾는다는 소리지요!
머신러닝에서 처음 배웠던 앙상블 개념이 이렇게 연결되니까 신기하네요 :)
● 6월 회고
6월에는 반 사람들과 두루두루 친해졌어요!
쉬는 시간마다 서로 간식도 나누고, 지식도 공유하면서 둥글둥글 지내고 있는데 정말 좋아요!!
뭔가 동물의 숲,,, 주민들 느낌이에요ㅋㅋㅋㅋㅋㅋㅋㅋ
다들 캐릭터 뚜렷하고 순둥한 느낌 들어서 그런지 더 동물의 숲 주민들 같아요ㅋㅋㅋㅋㅋ

휴... 이번 주에는 공부했던 내용들이 꽤나 난이도가 높네요....
저도 다시 복습해야 할 것 같습니다!
특히 옵티마이저 수식을 더 파악해 봐야겠어요!!
다음 주간도 힘내서 공부하겠습니다!!! 아자잣~~~
+) 부족한 부분이 있으면 댓글로 말씀해 주세요! 겸허한 마음으로 더 공부하겠습니다.
'활동 > SK네트웍스 Family AI 캠프 2기' 카테고리의 다른 글
| SK네트웍스 Family AI 캠프 2기 : 9th week (7월 2주차) (13) | 2024.07.15 |
|---|---|
| SK네트웍스 Family AI 캠프 2기 : 8th week (7월 1주차) (0) | 2024.07.08 |
| SK네트웍스 Family AI 캠프 2기 : 6th week (6월 3주차) (1) | 2024.06.24 |
| SK네트웍스 Family AI 캠프 2기 : 5th week (6월 2주차) (3) | 2024.06.16 |
| SK네트웍스 Family AI 캠프 2기 : 4th week (6월 1주차) (1) | 2024.06.09 |



